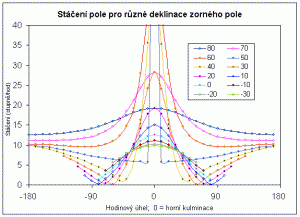
Pokud budeme fotografovat hvězdy s dalekohledem na azimutální montáži, tak i když budeme udržovat vybranou hvězdu ve středu pole, bude docházet ke stáčení zorného pole. Na některých částech oblohy je stáčení větší, někde menší. Nebylo by přeci jen možné fotografovat na azimutální montáži? Touto otázkou se zabývá následujíc článek.
A přece se stočí…!
Poznámka: Tohle povídání budiž přibližnou ukázkou toho, jak vzniká problém, jak se z něj destiluje jednoznačná úloha a jakými krkolomnými cestami se někdy dospívá k výsledku. Zároveň jest zde možno nahlédnout do originálních myšlenkových pochodů matfyzáka. Pokud vás zajímá jen výsledek, jděte rovnou na konec stránky.
Na Expedici v Bažantnici (rok 2003) mi Masek položil zdánlivě jednoduchý dotaz: Jak se bude stáčet zorné pole dalekohledu Meade. Takový dalekohled je na azimutální montáži a je naváděný v obou osách. Dodal ještě, že mi zatím neřekne, kdo si o tom co myslí, aby mě neovlivňoval. Protože jsem se právě vrátil z pokusného běhu s GPS, při kterém jsem naběhal přes osm kilometrů za dvě hodiny, v největším vedru, a našel jen čtyři kontroly z devíti, a to jedna byla startovní přímo v táboře, měl jsem v tuhle chvíli trochu jiné starosti. Nicméně problém jsem pochopil a slíbil že se nad ním příležitostně zamyslím. A skutečně. Poté, co jsem vypil tři litry vody, chrstnutím ešusu plného téže tekutiny ztrestal momentálně na karimatce spícího a nic zlého netušícího autora GPS-trasy, přátelsky s ním poklábosil o tom, kde ty kontroly vlastně byly, dal si svačinu a vypil další dva litry vody, jsem ucítil, že UŽ.
Tužku! Papír!
Tak, jak ono to je?
Kolem Polárky – míněno nebeského pólu – co to udělá? Tam to asi bude těch 15 stupňů za hodinu.
A když se jde dál?
No, tam se to asi nějak kazí. Deformuje.
Když budu mít hvězdu nad Polárkou -míněno nad pólem- tak za 6 hodin bude kde?
Když bude blízko tak přesně vpravo. 90 stupňů za 6 hodin. Jo.
A čím budu dál, tak co?
Co kdybych si zvolil ještě jednu hvězdu nad hvězdou nad polárkou? Potom za 6 hodin budou tyhle dvě hvězdy zase otočené o devadesát stupňů! Takhle to tada nepůjde.
Co kdybychom v myšlenkách přesídlili na pól? Pak máme polárku v nadhlavníku a azimutální montáž splývá s paralaktickou. Hurá! Máme první závěr: na pólu žádné stáčení pole nenastává. Jen aby to nebyla nějaká singularita.
A co na rovníku? Pohlédneme-li k tam k nebeskému pólu… který je na ideálním obzoru… vlastně můžeme koukat na oba, na severní na severu a na jižní na jihu… tak se to zase bude točit „magickou patnáckou“ (rozuměj 15 stupňů za hodinu). Ale vlastně u jižního pólu se to bude točit obráceně!
Je stáčení pole „fyzikálně hezkou“ funkcí? Čili funkcí bez singularit, funkcí hladkou, se všemi rozumnými derivacemi spojitými a to jak podle azimutu, výšky, času, hvězdného času i zeměpisné šířky? No doufejme, doufejme. Potom musí někde na rovníkové obloze ležet místo, vlastně minimálně celá izočára to musí být, kde je stáčení lokálně nulové. A metr od rovníku taky! A na pólu takové místo na obloze není! Takže existuje mezní zeměpisná šířka, kde se ještě na obloze dá najít místo bez stáčení! To jsem zvědavej, kde to bude! Poznámka po vyřešení: Na pólu se nulová izolinie rozleje na celou sféru.
Zpět na rovník: Hvězdy s nulovou deklinací… čili na nebeském rovníku… ty prostě stoupají a klesají! Když jsou takové dvě za sebou, tak se vezou za sebou. Tady se to nestáčí! Jenom při průchodu zenitem se prohodí. Ajajaj! Tam bude singularita! Nemáme ji tam ve středních zeměpisných šířkách taky? Máme! Ty dvě za-sebou-jdoucí hvězdy se sice zenitu blíží po obloučku a tak se vůči sobě nějak nenulově stáčejí, a najednou lup! Ta co byla dole je nahoře a zuřivý astronom se snaží ukroutit okulárový výtah.
Připomíná mi to jednu úlohu z Cvičení z astronomie ve třetím ročníku: Dvě hvězdy, jejichž deklinace se liší o tolik a tolik, jejich rekazcence zase o tolik. V zeměpisné šířce fí, jsou nad sebou a za dobu T budou zase nad sebou opačně. Určete deklinaci hvězd. Vlastně velmi podobná úloha. Vypotili jsme tenkrát vzorec, ale když jsme ho chtěli ověřit, ukázalo se, že má všude singularity – pro rovník, pro pól, pro hvězdy nad sebou, pro T=12 hodin. Nakonec jsme to ověřili empiricky ve skyglobu.
Dejme tomu, že už mám představu, jak se oblohová geometrie chová. Je čas požádat Maska, aby mi řekl, co si kdo o tom myslí. Jeho názor byl, že konstanta 15/hodinu bude stálá po celé obloze. Jirka Polák zase má pocit, že to bude pro každou hvězdu jiné, podle toho, jakou má deklinaci. Nuže, tento spor mohu rozhodnout už teď: Pravdu nemáte ani jeden. I pro jednotlivá hvězdná pole se bude rychlost stáčení měnit s časem, respektive s hodinovým úhlem. Ale jak, to bude na delší výpočet. Až ho udělám, tak vám výsledek pošlu.
A šli jsme na večeři a pak přihlížet modelářským aviatikům a večer na kopec pozorovat blesky a pak jsem odjel z expedice domů. Asi po týdnu jsem se k problému vrátil.
No co, to bude jednoduchý. Prostě si odvodím vzorec stáčení pole =… co bude na pravé straně? No nějaká funkce, ale čeho. Zeměpisné šířky (?) určitě. A souřadnic místa na obloze, nejjednodušší bude deklinace (?) a hodinového úhlu (t). Co ten hodinový úhel je? Něco jako rekazcenece, ale na jihu je to prostě nula. Myslím že se to na sebe převádí přes hvězdný čas. Jedna z těch veličin plus něco jiného je ta třetí.
No, tak zjistíme jak je taková hvězda vysoko a taky azimut (bude lepší si tam představovat hvězdu, říkejme jí středová). Pak si zvolím jinou hvězdu o nějaké malé ?? a ? vedle a zjistím to pro ní. Z rozdílu azimutů a výšek mi vyjde sklon spojnice těch dvou hvězd k obzoru. Pak to celé zderivuju podle času a budu mít rychlost stáčení pole. A když budu chtít, převedu to zpátky do obzorníkových souřadnic. Tam si pak můžu derivovat, hledat minima a maxima podle lokální výšky, azimutu i zeměpisné šířky! Joj! Jak prosté, milý Watsone!
Krok první, převod nebeských a topocentrických souřadnic. To je přece brnkačka. To je otočení podle nějaké osy… půl hodiny čmárání obrázků, až je zřejmé, že nejlepší bude osu x namířit k východu, y k severu a z nahoru. Tož otočíme o „90-?“, u kterého sinu v rotační matici bude to mínus? Tak ho dáme třeba sem. No, hezká dvojice vzorečků:
sin(h) = sin(?) sin(?) + cos(?) cos(?) cos(t)
cotg(A) = cotg(t) sin(?) – ( tg(?) cos(?) / sin(t))
Tak teď to samé, ale pro posunutou hvězdu. Hele, to pole se točí jako celek, tak si můžeme vybrat nějakou speciální hvězdu, ta co má jen o ?? větší deklinaci se přímo nabízí. Takže ? dáme pryč, je to nula.
sin(h+?) = sin(?+??) sin(?) + cos(?+??) cos(?) cos(t+?)
cotg(A+?) = cotg(t+?) sin(?+??) – ( tg(?) cos(?+??) / sin(t+?))
Odečíst „nedeltové“ vzorečky od „deltových“ a podíl ?/? je uz tangens náklonu! Hm, bude potřeba se té delty deklinace zbavit, na té to přece nesmí záležet. -Půl hodina odvozování a následného hledání součtových vzorců v tabulkách.- Teď to jen správně zanedbat. Sinus malýho je nula, kosinus malýho je jedna. Snad to nepřeháním. Hm, asi jo, to by mi vyšla blbost. Tak sinus necháme. Akorát tangens je teď to samý jako sinus. Hurá, vyrušilo se to, nejní to úplně mimo mísu.
? = ?? . (cos(t)sin(?)-sin(?)cos(?)cos(t)) / cos(h)
? = ?? . (sin(t)+cotg(A)cos(t)sin(?)+tg(?)cos(?)) / (cos(?)+cotg(A)tg(?)sin(t))
tg(?) = ?/?
Výborně, ?? v hodnotě stočení pole mizí, pole se točí jako celek. Teď to ještě zderivovat a zjednodušit. Po dvou A4 vzorec pro stáčení pole odvozen, ale zjednodušení se nedaří. Zlomková čára se táhne přes celou stránku. Derivací se jmenovatel prodloužil nad únosnou míru a zbavování se deklinace způsobilo jednu odmocninu. Na převod do obzorníkových souřadnic mi nezbývá síla. Natož na nějaké vyšetřování průběhů funkce podle různých parametrů. Přímočaré řešení končí v močálech…
O měsíc později se při úplně jiné činnosti dostavuje záblesk inspirace: Když to nešlo analyticky, co to vzít hrubou silou? To je přece základní pravidlo práce s laboratorním přístrojem: „Nenamáhej se zbytečně, vezmi si větší kladivo.“
Větším kladivem je v tomto případě počítač. Jednoduchý program mám za dvě hodiny napsaný a v podstatě i odladěný (rozuměj: ty čísla co z něj padají vypadají v pořádku). Hrome, to je brutální, derivovat takhle přímočaře. Delty zvolíme jedna, když už jedeme v úhlových vteřinách. Však ona to ta plovoucí desetinná čárka vydrží. Vydržela.
Odhalil jsem ještě jednu slabinu mých starých výpočtů, totiž že azimut je potřeba na konci dělit kosinem výšky. Vede to k paradoxnímu (ale správnému) „matematickému“ jevu: Představte si hvězdu jeden stupeň od pólu, má tedy deklinaci 89 stupňů. Jaké jsou meze jejího výskytu během jedné otáčky Země, pozorováno z 50 stupně severní šířky? Výškově to sedí, hvězda je vždy mezi 49 a 51 stupni vysoko, ale v azimutu ne. Její maximální azimut „vpravo“ není 1 stupeň, protože výšková kružnice (neříká se jí almukantarant?) není kružnicí hlavní. A tak, ačkoli je jen stupeň od nebeského pólu, který má z definice azimut nula, azimut hvězdy je 1 stupeň a 33 minut! Konec konců, stačí se podívat do hvězdářské ročenky na zdánlivě nudnou tabulku „Výška a azimut polárky“. Je to tam!
Ale dosti hledání paradoxů, podívejme se na výsledky: Kolem pólu je to opravdu blízko magické patnáctky. A pro hvězdy jdoucí kolem zenitu to hodně roste. A u obzoru to naopak klesá hluboko pod deset stupňů za hodinu. Nejvíc na východě a na západě. Jak je to asi srovnané po obloze? Zdá se, že kolem zenitu bude nějaký „koláč“ ukrutně vysokých hodnot.
Graf absolutní velikosti stáčení pro pole různé deklinace během denního oblouku byl získán interpolací hodnot (malá kolečka na křivkách) po 10 stupních v hodinovém úhlu (40 minut časových). Graf trochu lže – tam kde se křivky (téměř) dotýkají nuly se mění směr stáčení. Krátké obloučky nad jihem (deklinace záporná) mají v reálu opačné znaménko – pole se otáčí po směru hodinových ručiček. Data jsou omezena na ty hodnoty, kdy je dané pole nad obzorem.
Za povšimnutí stojí to, jak pole kulminující blízko zenitu vykazují obrovské hodnoty stáčení. Stáčení roste tak, že nemá smysl uvádět přesná čísla.
Jak ale zviditelnit rozložení po sféře, když data jsou ve formátu delta – hodinový úhel – stáčení ? Tak přerubeme výstupy a spočítáme ještě jednou azimut, výšku a k tomu stáčení. Chtělo by to graf v polárních souřadnicích. Umí to Excel? (Půlhodina vyčerpávajícího boje se softwarem…) Neumí. Problém uložen k ledu na další měsíc(e).
Během konzultací s těmi, kteří si to vymysleli dospívám k závěru, že hvězdná pole na obloze lze rozdělit na dvě kategorie:
Krouživá pole, které za 24 hodin provedou v azimutálním dalekohledu celou otáčku a jejich průměrná rychlost stáčení je 15 st/h. Neopustí severní polovinu oblohy (polosféru) a kulminují dvakrát, jednou horně mezi pólem a zenitem, podruhé spodně, to už však ne nutně nad obzorem. Směr jejich stáčení je stále stejný (na severní polokouli proti směru hodinových ručiček), rychlost může kolísat. Při poloze stanoviště na zeměpisném rovníku jsou taková pole na celé obloze.
Kývající se pole, jejichž směr stáčení se během otáčky 2x změní. V okamžicích změny směru stáčení je rychlost stáčení nulová. Jedna kulminace takového pole nastává na jižní polovině hlavní poledníkové kružnice, druhá na severní polovině. Během otáčky pole oběhne (obecně velmi excentricky) spojnici zenit-nadir, tj. lokální svislici.
Přechodem mezi polemi krouživými a kývacími jsou ta, jejichž deklinace je právě rovna zeměpisné šířce stanoviště. Taková procházejí zenitem a co se děje tam, to se těžko popisuje. Zenit nemá azimut, při dělení kosinem výšky nastává dělení nulou, prostě singularita jako prase. Co by udělal dalekohled, když se ho pokusíme na takové pole navést? Musí se otočit o 180 stupňů kolem svislé osy v okamžiku, kdy bude koukat do zenitu. Jinak by jel dál do výšek „nad 90 stupňů“, až by se mu zkroutily kablíky. A podle toho, kterým směrem dalekohled rotaci provede se rozhodne, jestli tento limitní případ přiřadí ke krouživým nebo kývacím polím.
Hleďme, zajímavá informace: VLT, dalekohled s průměrem zrcadla 8 metrů, má v zenitu „blind spot“, slepou skvrnu. Takže se koukání do zenitu nedovoluje. Nakonec i meteorologové na Libuši, když navádějí své paraboly za přelétávajícími družicemi už řešili tenhle problém.
O několik týdnů později: Co je to za prográmek? Ten přece dělá bitmapu, pěkně pixel po pixlu, podle toho co se mu řekne. To by šlo zmodifikovat na libovolnou velikost, že jo? A když tam dám výpočet stáčení pole, tak si ho můžu vytáhnout v jakém tvaru budu chtít. Tak jdem na to! Azimut a výška se převede na x,y, teď to správně přeškálovat na rozměr obrázku. Udělám to 2 pixely na stupeň, takže oblohu splácnu do 360×360 pixelů. Je sever nahoře? Jo. To je ale zvláštní obrázek. Tak ještě oškálovat a můžeme drtit. Jemnost barev po 5 st/h bude stačit. Tři odstíny modré pro stáčení pomalejší než 15 st/h, pak zelená pro 15-20, žlutá 20-25, oranžová 25-30 a dvě červené pro 30-35 stupňů v hodině a více.
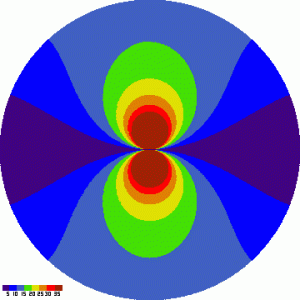
Nakreslil jsem si rozložení rychlosti stáčení pole po obloze pro zeměpisné šířky 0,25,50 a 75 stupňů. Tady jsou:
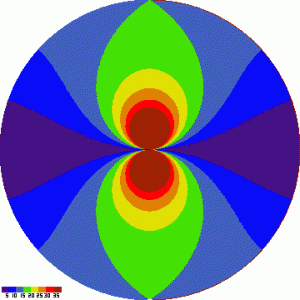 |
Zem. šířka 0 stupňů – rovník |
 |
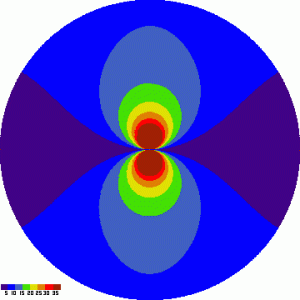
Zem. šířka 25 stupňů |
 |
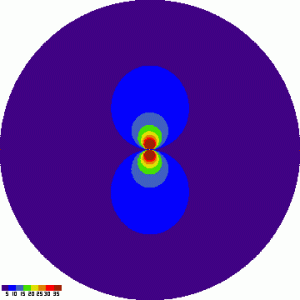
Zem. šířka 50 stupňů |
 |
Zem. šířka 75 stupňů |
Sever je nahoře, jih dole, východ vlevo a západ vpravo, jak je na mapách oblohy zvykem. Uprostřed je zenit.
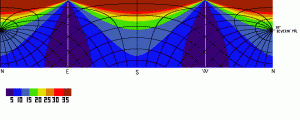
Pro ty ilustraci ještě jeden obrázek pro 50 stupňů šířky, tentokrát rozložený na válec.
Celá horní hrana obdélníku je zenit. Pomocné černé čáry jsou paralaktické souřadnice po 15 stupních. Čáry konstantní deklinace ukazují, jak se mění velikost stáčení pole na různých deklinacích během denního oblouku.
Obrázky ukazují věci které jsem tušil i některé, které mi unikly. Celé stáčení je symetrické kolem linie východ-západ. Čili v bodě „naproti polárce“ (rozuměj u nás 50 stupňů nad jihem) je stáčení 15 stupňů za hodinu (byť na opačnou stranu). Linie kde je stáčení právě rovno 15 stupňů za hodinu je na obrázcích hranice mezi modrou a zelenou. Tvoří ji dva vejcovité útvary, jejichž krajní body ve výšce nad obzorem jsou zenit (90 st) výška nebeského pólu (rovna zeměpisné šířce stanoviště). Další důležitou linií je „nulová“ čára, hlavní kružnice spojující východní obzor, zenit a západní obzor. To co je v severní polovině oblohy (pokud uvažujeme neprůhledný obzor, tak v čtvrtkouli V-S-Z-zenit) se stáčí proti směru hodinových ručiček, vše co je v jižní polovině oblohy naopak ve směru hodinových ručiček. Při pozorování východním nebo západním směrem, tj. v azimutu 90 nebo 270 stupňů se stáčení pole nevyskytuje! V praxi ale, pokud nejsme na pozemském rovníku, nám hvězdné pole tuto linii pouze protne. Přesto je výhodné pozorovat (fotografovat) právě tam.
Nadprůměrné stáčení pole je naopak v oblasti mezi nebeským pólem a zenitem a paradoxně také na opačné straně zenitu. Pokud by někdo chtěl tento jev demonstrovat fotografií, tak nejvyšší hodnoty jsou v blízkosti zenitu, avšak pozor, pouze směrem k pólům, směrem k východu a západu naopak ne.
Zenit naopak má ty nejnemožnější vlastnosti: V jeho těsném (infinitezimálním) okolí lze najít libovolnou hodnotu stáčení od nuly až kam si vzpomenete, takže nelze tamní hodnotu stáčení ani dodefinovat. Zřejmě kolem něj musí být zmiňovaná slepá skvrna, která zabraňuje havárii dalekohledu (ať už softwarové nebo kablíkové).
A když už tedy víme, jak se pole v dalekohledu stáčí, zbývá navrhnout protiopatření pro ty, kterým to vadí:
1) Pořiďte si paralaktickou kolébku a změňte tak svou azimutální montáž v paralaktickou.
2) Odstěhujte se pozorovat na pól. (Bystrý čtenář jistě poznal, že tato rada je ekvivalentní s předchozí.)
3) Exponujte krátké časy, u nichž se otočení nestačí projevit.
4) Pozorujte hvězdy na východě nebo na západě. Čím blíž rovníku, tím déle vám tam pole vydrží.
5) Pořiďte si otočnou redukci a dodělejte si k ní motor a software, které šišatost nebeské klenby srovná.
6) Redukci s předchozího bodu řiďte ručně. Tak jako dříve hvězdáři naváděli dalekohled na bod pointováním, rád bych v obrozeneckém duchu nazval tuto činnost angulování, respektive angulace. Je samozřejmé, že místo pointačního dalekohledu budete používat dalekohled angulační. Jenom ten záměrný kříž může být stejný.
Honza Mocek
Ověření teorie
H+P Plzeň vlastní dva dalekohledy Meade na azimutální montáži a přestože k oběma máme paralaktické kolébky, používáme prakticky pouze montáž azimutální. Důvodem je hlavně rychlost ustavení montáže, které pro azimutální montáž trvá 5 minut, zatímco pro paralaktickou několik hodin. Na vizuální pozorování je přitom azimutální montáž vyhovující. Problém nastane při fotografování.
Přestože to Honza velice dobře teoreticky odvodil, zajímalo mě, zda by přeci jenom nešlo využívat azimutální montáž na fotografování, třebas jen na místech, kde je stáčení pole nejmenší. Navíc jsem si chtěl prakticky ověřit, jak je to opravdu se stáčením pole.
Všechny snímky jsou pořízeny v primárním ohnisku dalekohledu Meade 200/2000mm digitálním fotoaparátem Canon EOS 10D s nastavenou citlivostí 100ASA. Zorné pole vychází 40′x25′. Nejslabší hvězdy mají při 5 minutové expozici kolem 10 magn. Pointační hvězda se nachází 26′ pod středem snímku. Přesnou pointaci na hvězdu zajišťoval autopointer Meade 201XT zasunutý v mimoosovém T-hranolu. Tento autopointer velice přesně drží vybranou hvězdu, která se nachází asi půl zorného pole pod fotografovaným polem. Stáčení hvězd probíhá potom kolem této hvězdy.
Naměřené výsledky celkem dobře odpovídají teorii. V určitých místech oblohy je opravdu možné dělat kratší expozice na azimutální montáži. Problémem zůstává složitost stáčení, která se dá dost těžko odhadnout a výsledek na azimutální montáži je proto vždy nejistý. Na fotografování se paralaktická kolébka ukazuje jako nutnost.